Journal Publications
Realizability-preserving discontinuous Galerkin method for spectral two-moment radiation transport in special relativity
In this paper, we introduce a robust discontinuous Galerkin, implicit–explicit method for special-relativistic two-moment radiation transport. Built on a maximum-entropy closure, the scheme is carefully designed to preserve moment realizability, ensuring physically meaningful solutions, while accurately modeling massless particle transport in relativistically moving media. A suite of numerical tests demonstrates both the accuracy and stability of the approach.
DG-IMEX Method for a Two-Moment Model for Radiation Transport in the O(v/c) Limit
In this paper, we propose a DG-IMEX method to evolve a spectral two-moment model for particles interacting with a background fluid moving with nonrelativistic velocities. The system of nonlinear moment equations includes velocity-dependent terms that account for spatial advection, Doppler shift, and angular aberration. The method is designed to preserve moment realizability, which guarantees that the moments correspond to a nonnegative phase-space density. In time integration, nonlinearity of the moment model necessitates solution of nonlinear equations, which are solved with tailored iterative solvers that preserve moment realizability with guaranteed convergence. We also investigate the simultaneous Eulerian-frame number and energy conservation properties of the proposed scheme.
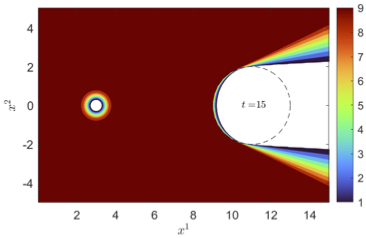
A Parametric Study of the SASI Comparing General Relativistic and Non-Relativistic Treatments
We investigate the effects of general relativity (GR) on the standing accretion shock instability (SASI). We perform ten axisymmetric simulations: five with GR hydrodynamics and gravity and five with non-relativistic (NR) hydrodynamics and gravity. We find that the use of GR leads to a slower SASI growth rate and a longer SASI oscillation period than NR.
thornado-hydro: a discontinuous Galerkin method for supernova hydrodynamics with nuclear equations of state
This paper describes the methods implemented in thornado for solving the equations of nonrelativistic hydrodynamics with self-gravity and a tabulated nuclear equation of state. We provide descriptions of the discontinuous Galerkin spatial discretization, strong stability-preserving Runge-Kutta time integration, and limiters necessary for a stable evolution. A suite of hydrodynamics tests are performed to show the accuracy and stability of thornado. To test the implementation on a problem of relevance to core-collapse supernovae, we apply thornado to the adiabatic gravitational collapse of a 15 solar mass progenitor, following the evolution through collapse, bouce, and hundreds of milliseconds of shock propagation.
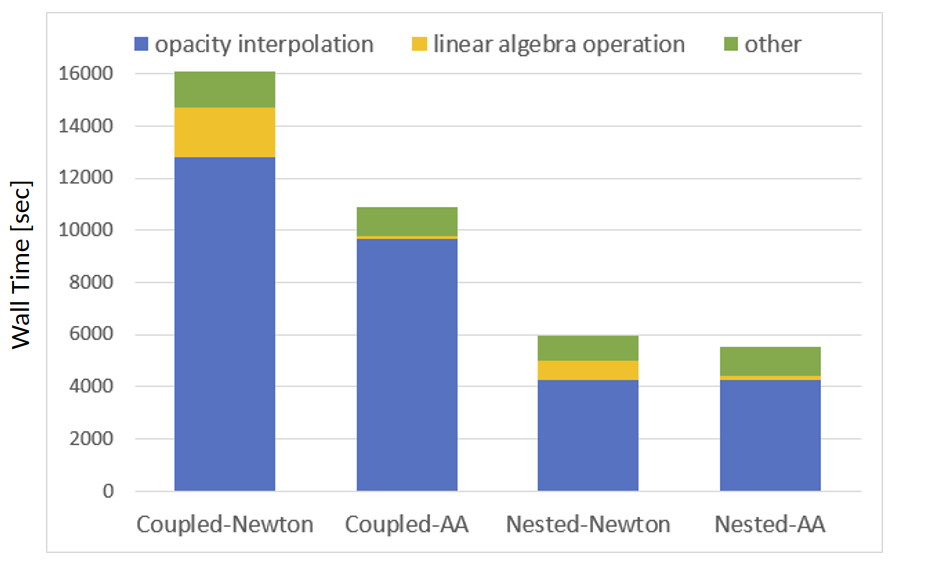
A DG-IMEX Method for Two-moment Neutrino Transport: Nonlinear Solvers for Neutrino–Matter Coupling
In this paper, we design and compare nonlinear iterative solvers for implicit systems with energy-coupling neutrino–matter interactions. The implicit systems arise from the discretization of a two-moment model, which employs the discontinuous Galerkin method for phase-space discretization and implicit–explicit time integration. We propose coupled and nested approaches to formulate the nonlinear systems. For each approach, the resulting systems are solved with Anderson-accelerated fixed-point iteration and Newton’s method. The performance of these four iterative solvers are compared on relaxation and proto–neutron star deleptonization problems. Numerical results suggest that the nested Anderson-accelerated fixed-point solver is more efficient than other solvers for solving implicit nonlinear systems with energy-coupling neutrino–matter interactions.
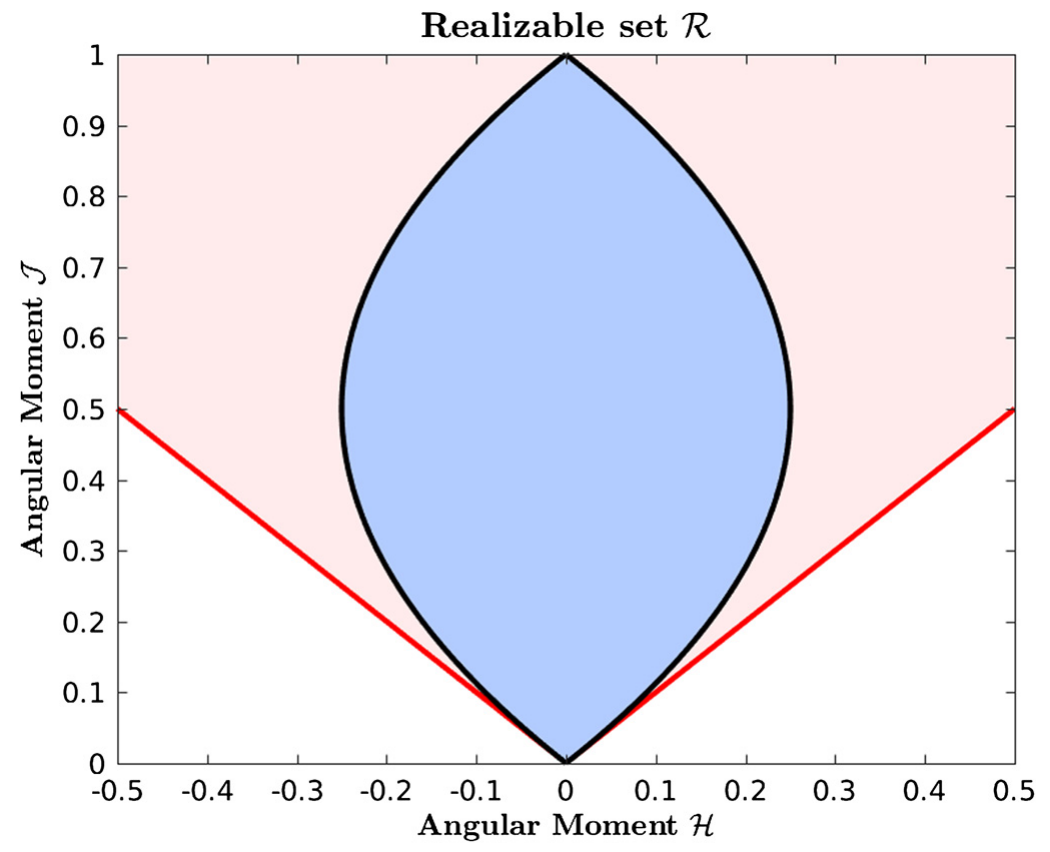
Realizability-preserving DG-IMEX method for the two-moment model of fermion transport
In this paper, we develop a realizability-preserving method to simulate the transport of fermions through a static background material using a two-moment model, which is closed using algebraic closures. We employ the discontinuous Galerkin method for spatial discretization combined with implicit-explicit time integration. Special care is taken to ensure the method preserves strict algebraic bounds on the evolved moments as dictated by Pauli’s exclusion principle. Numerical results demonstrate the realizability-preserving properties of the scheme, and we demonstrate that the use of algebraic moment closures not based on Fermi-Dirac statistics can lead to unphysical moments in the context of fermion transport.
Preprints and Manuscripts
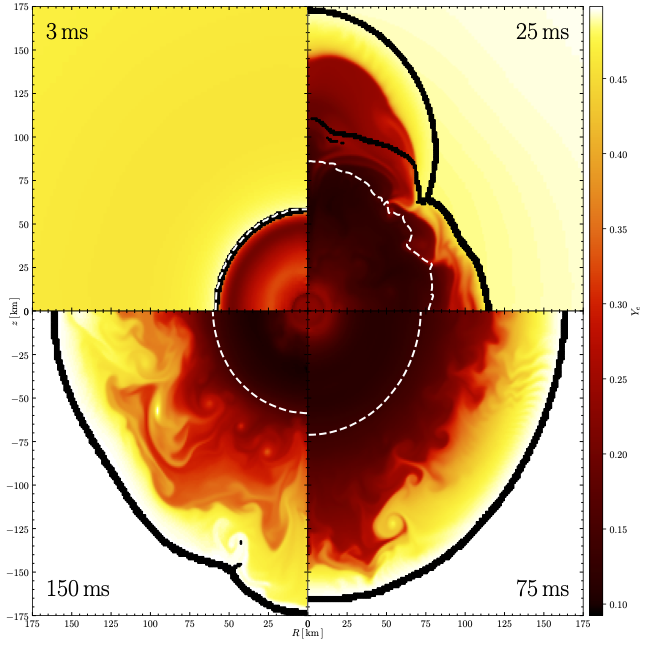
thornado+Flash-X: A Hybrid DG-IMEX and Finite-Volume Framework for Neutrino-Radiation Hydrodynamics in Core-Collapse Supernovae
In this paper, we describe thornado’s O(v/c) neutrino-transport algorithms and their coupling to self-gravitating hydrodynamics within the AMR-based Flash-X framework. The code combines a spectral, multi-species two-moment formulation with discontinuous Galerkin discretization, fully implicit neutrino–matter coupling, and GPU acceleration. Verification tests and 1D/2D core-collapse supernova simulations demonstrate accuracy, robustness, and strong agreement with the established core-collapse supernova (CCSN) code Chimera, demonstrating the viability of thornado’s DG-based neutrino transport for multidimensional CCSN simulations.
Conference Proceedings
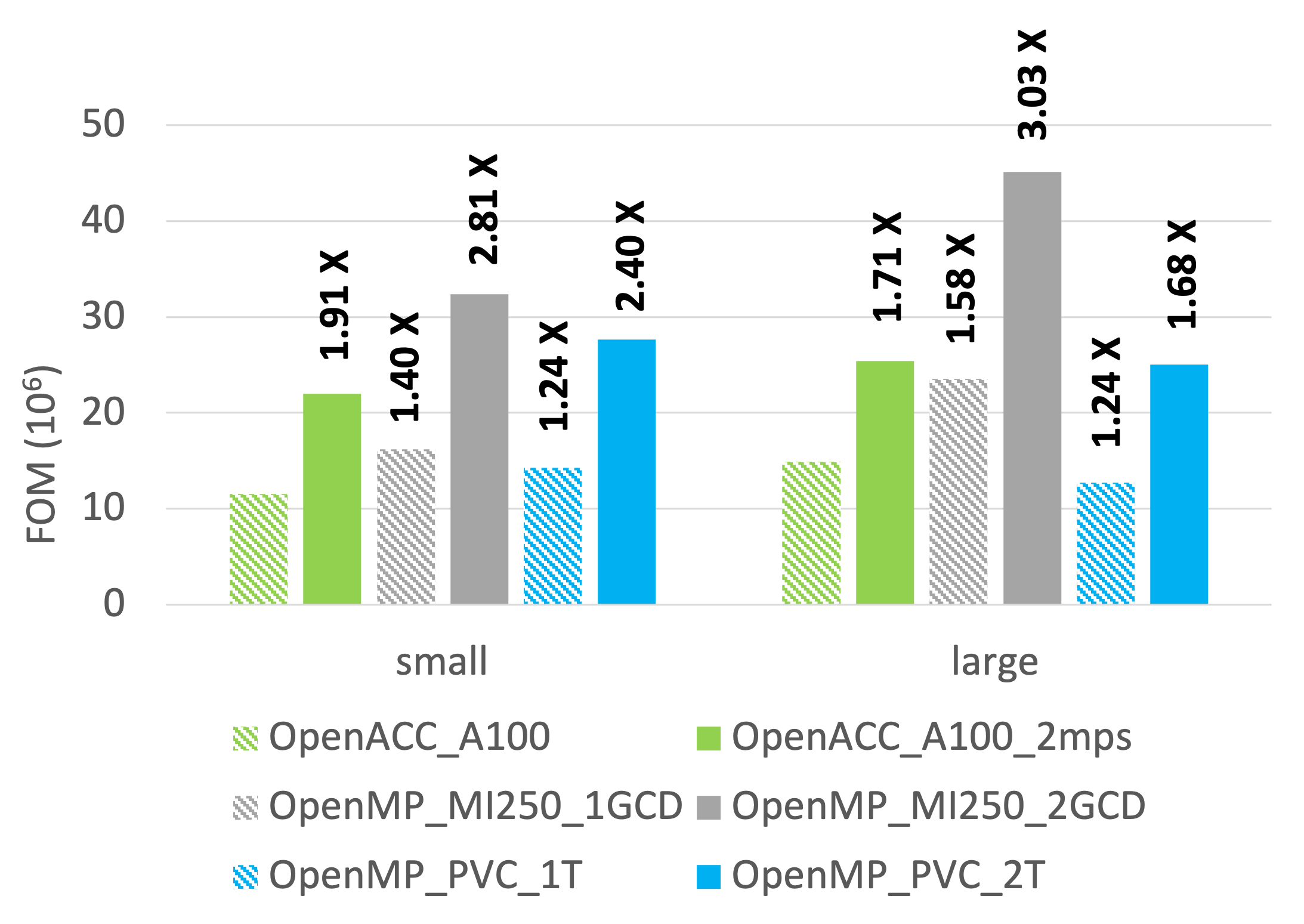
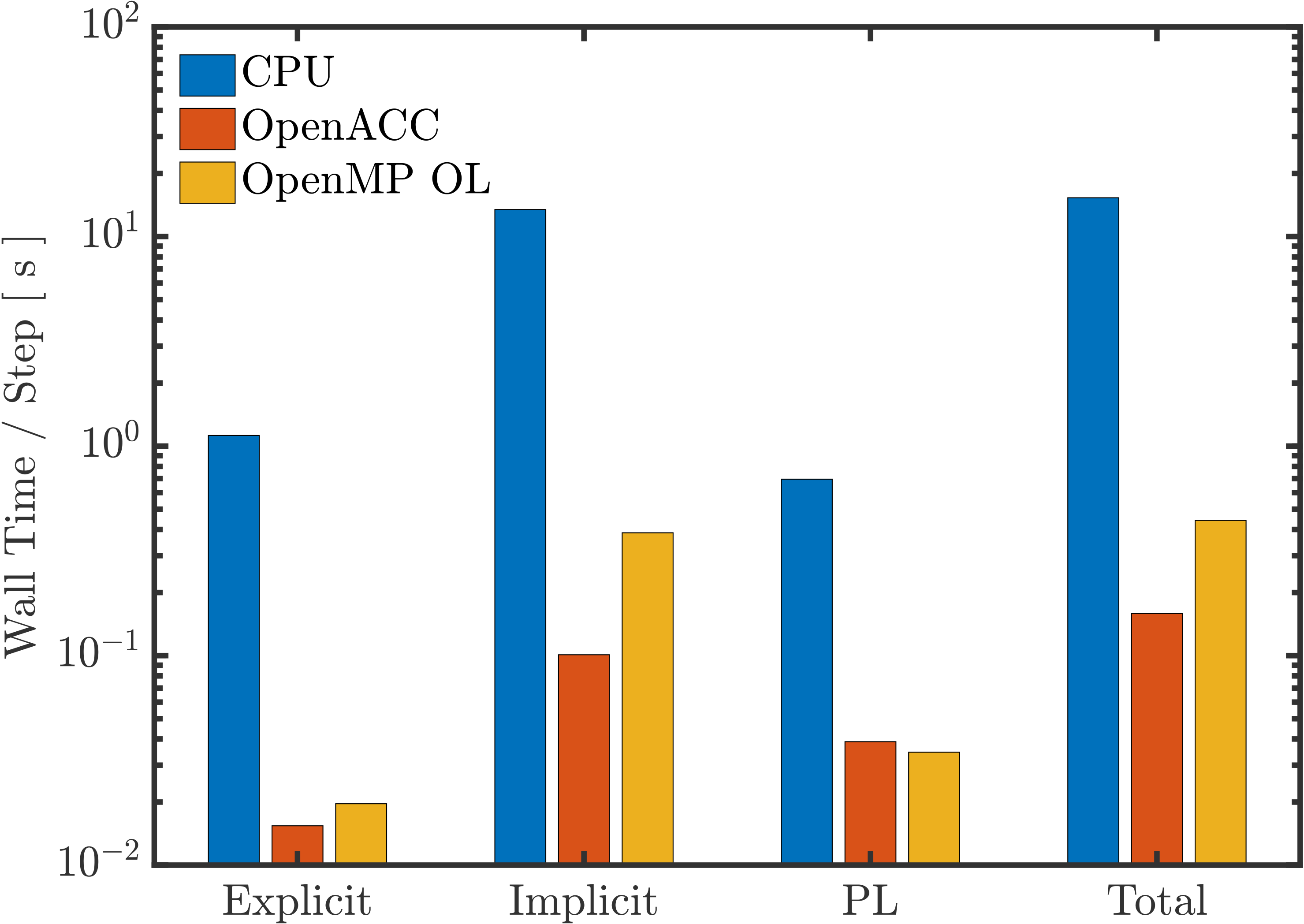
Performance Porting the ExaStar Multi-Physics App Thornado On Heterogeneous Systems - A Fortran-OpenMP Code-Base Evaluation
In this work, we evaluate the computing capability of heterogeneous systems for thornado using Fortran with OpenMP and the performance portability of the astrophysical supernova simulation code Flash-X on heterogeneous systems. For this study, three HPC systems were chosen: 1) Sunspot, a test-bed system of the Intel-PVC GPU featured supercomputer Aurora; 2) Polaris, an NVIDIA system accelerated by A100 GPUs; and Frontier, an AMD-MI250-based system. We discuss challenges and solutions for performance porting the compute-intensive module thornado, which can be incorporated as an external library in Flash-X to model neutrino transport. We show that the performance of test apps improved by approximately 24$\times$ using the relevant optimization strategies with compiler-and-system updates. Further, this study helped improve the intel OneAPI-OpenMP compiler by providing bug reports and reproducers internally.
Access: DOI
thornado-transport: Anderson- and GPU-accelerated nonlinear solvers for neutrino-matter coupling
Algorithms for neutrino-matter coupling are investigated in the context of a spectral two-moment model, discretized with discontinuous Galerkin and implicit-explicit methods, and implemented in thornado. The model considers electron neutrinos and antineutrinos and tabulated opacities from Bruenn (1985). The nonlinear system arising from implicit time discretization of the equations governing neutrino-matter coupling is iterated to convergence using Anderson-accelerated fixed-point methods, which avoid formation of Jacobians and inversion of dense linear systems. Our initial port to GPUs, using both OpenMP and OpenACC, shows an overall speedup of up to ∼ 100x when compared to results using a single CPU core. These results indicate that the algorithms implemented in thornado are well-suited to GPU acceleration.
Access: DOI
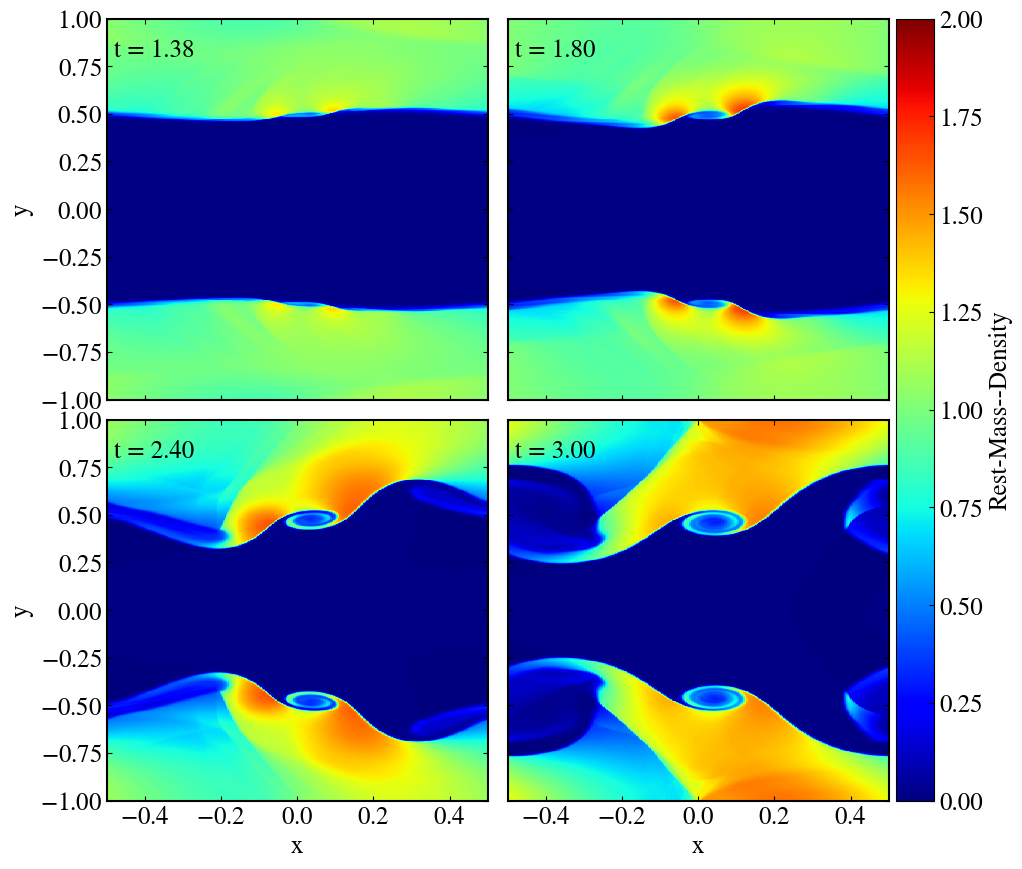
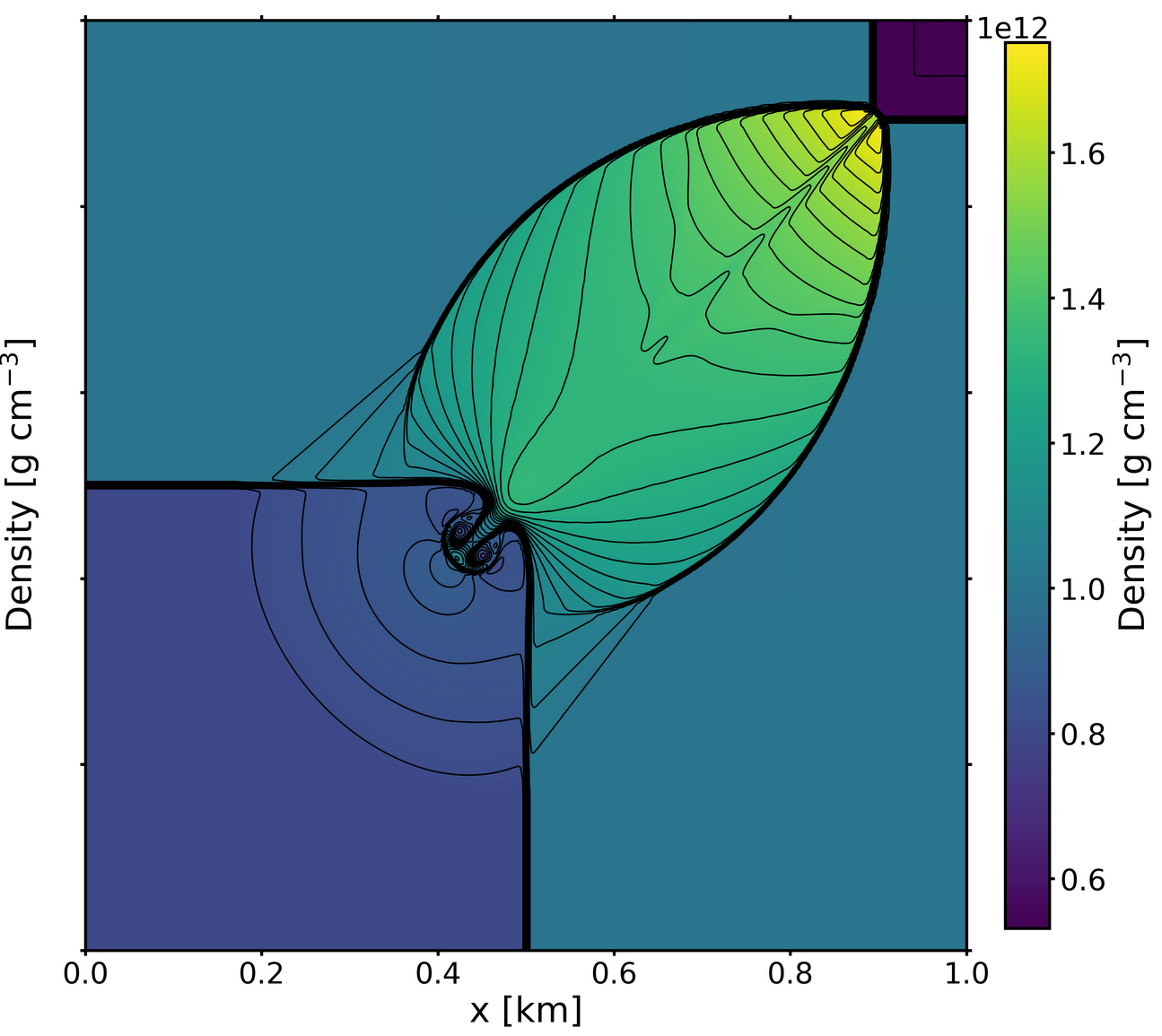
A discontinuous Galerkin method for general relativistic hydrodynamics in thornado
During the 2019 ASTRONUM conference, we discussed progress in the development of our solver for the general relativistic hydrodynamics equations using DG methods under the conformally flat condition, a sophisticated approximation to GR. We verify the accuracy and robustness of our code with several difficult test-problems: a special relativistic Kelvin–Helmholtz instability problem, a two-dimensional special relativistic Riemann problem, and a one- and two-dimensional general relativistic standing accretion shock problem. We find good agreement with published results, where available.
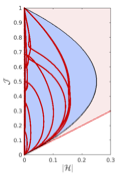
thornado-transport: IMEX schemes for two-moment neutrino transport respecting Fermi-Dirac statistics
This paper discusses implicit-explicit (IMEX) time stepping schemes for neutrino transport in the context of a two-moment model. Pauli’s exclusion principle constrains the moments to a closed convex set, and convex-invariant time steppers play a role in the design of methods that respect these constraints. Two convex invariant IMEX Runge-Kutta schemes are presented that work well in the diffusion limit and reduce to optimal second- and third-order explicit strong stability-preserving Runge-Kutta methods in the streaming limit. The performance of the IMEX schemes is demonstrated in numerical tests using a DG method with third-order spatial discretization.
Access: DOI
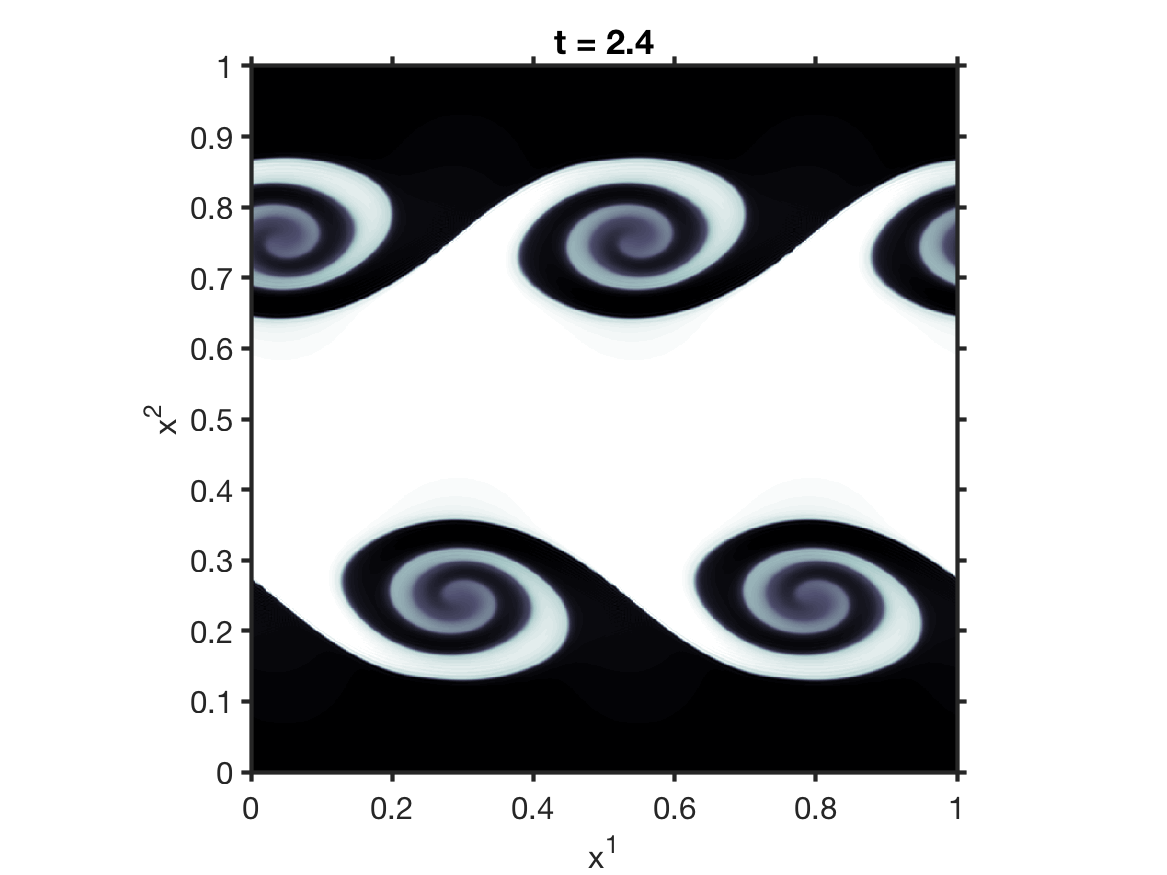
thornado-hydro: towards discontinuous Galerkin methods for supernova hydrodynamics
In this paper, we provide an overview of the numerical methods for the Euler equations — in non-relativistic and special relativistic limits — in thornado, and present preliminary numerical results from a set of basic tests in one and two spatial dimensions.
Access: DOI
Theses
General Relativistic Gravity in Core-Collapse Supernova Simulations
James Nicholas Roberts II, PhD Dissertation, University of Tennessee Knoxville, 2024. Access: DOI
thornado-Hydro, xCFC: A Discontinuous Galerkin Hydrodynamics Solver for General Relativistic Core-Collapse Supernova Simulations
Samuel J. Dunham, PhD Dissertation, Vanderbilt University, 2024. Access: DOI
Core-Collapse Supernova Simulations with Spectral Two-Moment Neutrino Transport
Ran Chu, PhD Dissertation, University of Tennessee Knoxville, 2022. Access: DOI
Use of thornado in Other Software
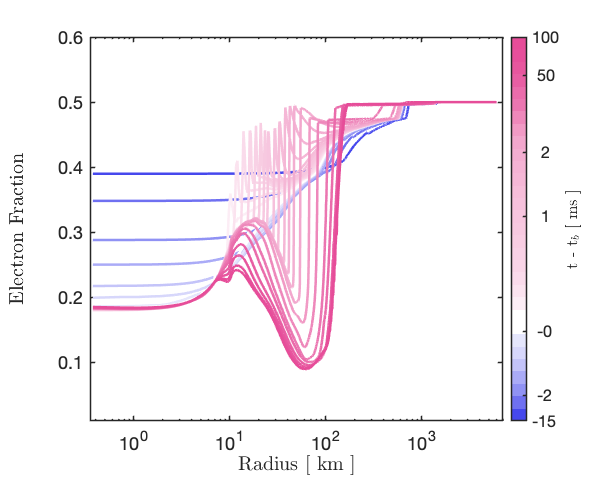
Exascale models of stellar explosions: Quintessential multi-physics simulation
This paper describes the ExaStar project’s aims to deliver a portable software ecosystem for multi-physics astrophysics simulations run on exascale machines. It provides and overview of the incorporation of thornado in Flash-X, including (1) coupling of thornado’s neutrino transport (based on DG methods) with Flash-X’s self-gravitating hydrodynamics (based on finite-volume/finite-difference methods); (2) the strategy for porting thornado to GPUs, and (3) preliminary results from a core-collapse supernova simulation in spherical symmetry with Flash-X and thornado.